Statistical procedures are called robust if they remain informative and efficient in the presence of outliers and other departures from typical model assumptions on the data. Ignoring unusual observations can play havoc with standard statistical methods and can also result in losing the valuable information gotten from unusual data points. Robust procedures prevent this. And these procedures are more important than ever since currently, data are often collected without following established experimental protocols. As a result, data may not represent a single well-defined population. Analyzing these data by non-robust methods may result in biased conclusions. To perform reliable and informative inference based on such a heterogeneous data set, we need statistical methods that can fit models and identify patterns, focusing on the dominant homogeneous subset of the data without being affected by structurally different small subgroups. Robust Statistics does exactly this. Some examples of applications are finding exceptional athletes (e.g. hockey players), detecting intrusion in computer networks and constructing reliable single nucleotide polymorphism (SNP) genotyping.
Recent Highlights
Robust Functional Data Analysis
M. Salibián-Barrera
Functional Data Analysis methods require some kind of regularization or dimension reduction. Functional Principal Components is one of the most popular such techniques due to its interpretable features, which are often explored on their own or used in subsequent analyses. In recent work, Professor Salibián-Barrera, with collaborators Boente and Tyler, has shown how to rigorously define and estimate Functional Principal Components under weaker regularity assumptions (e.g. heavy tails, or outlier contaminations), and how their properties and interpretations compare with those of their "classical" counterparts.
Read the JASA Paper JASA GitHub Read the JMVA Paper Read the METRON Paper METRON GitHub
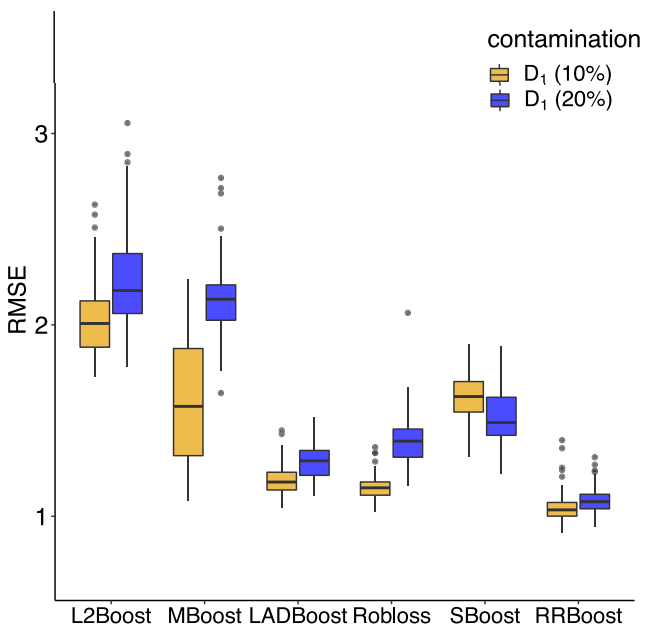
Robust and Scalable Non-Parametric Regression
M. Salibián-Barrera
Gradient boosting algorithms for regression provide flexible predictors for continuous response variables. However, training these models when the data may contain atypical observations (outliers) presents delicate conceptual and computational challenges. In a new paper, Professor Salibián-Barrera and Ph.D. student X. Ju have tackled the issue of robust boosting without the need for ad-hoc residual scale estimators typical of past work.