The Bayesian paradigm for statistical inference uses expert knowledge, formulated in terms of probability distributions of unknown parameters of interest. These distributions, called prior distributions, are combined with data to provide new information about parameters, via new parameter distributions called posterior distributions. One research theme centers on devising new Bayesian methodologies, i.e., new statistical models with which Bayesian inferences can provide particular scientific insight. Quantifying the statistical properties of such methods and contrasting with non-Bayesian alternatives is an active area of research. Bayesian methods can lead to computational challenges, and another research theme centers on efficient computation of Bayesian solutions. The development of computational techniques for determining posterior distributions, such as Monte Carlo methods, is a rich area of research activity, with particular emphasis on Markov Chain Monte Carlo methods and sequential Monte Carlo methods.
Recent Highlights


Pigeons.jl: Distributed Parallel Tempering
A. Bouchard-Côté, T. Campbell
Pigeons is a Julia package used to estimate expectations of challenging posterior distributions, and more broadly, approximately solve Lebesgue integration problems. Pigeons can be used in a multi-threaded context, and/or distributed over hundreds or thousands of MPI-communicating machines. Principal Investigators Bouchard-Côté and Campbell (in collaboration with P. Gagnon at U de M and L. Wang at SFU) were awarded a 2025 CANSSI Collaborative Research Teams grant for this project.
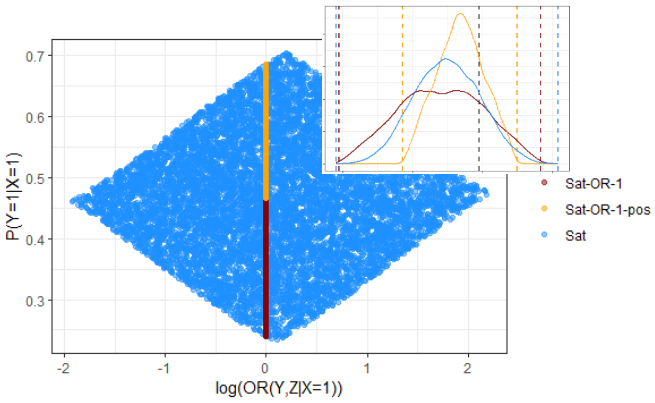
Partial identification for discrete data with nonignorable missing outcomes
P. Gustafson
Nonignorable missing outcomes are common in real world datasets and often require strong parametric assumptions to achieve identification. These assumptions can be implausible or untestable, and so we may forgo them in favour of partially identified models that narrow the set of a priori possible values to an identification region. In recent work, Professor Gustafson and collaborator Daly-Grafstein have proposed a new nonparametric Bayes method that allows for the incorporation of multiple relevant restrictions of the parameter space simultaneously, including instrumental variables and the direction of missing data bias.
